RANGKAIAN ARUS BOLAK BALIK

Arus bolak-balik atau altenating current (AC) merupakan arus dan tegangan listrik yang besarnya berubah terhadap waktu dan mengalir dalam dua arah. Arus bolak-balik biasanya dimanfaatkan untuk peralatan elektronik. Sumber arus bolak-balik prinsip kerjanya yaitu terjadi perputaran kumparan dengan kecepatan sudut tertentu yang berada dalam medan magnetik. Jenis-jenis rangkaian dalam rangkaian AC adalah rangkaian resistor, rangkaian induktor, dan rangkaian kapasitor.

Rangkaian Arus Bolak Balik

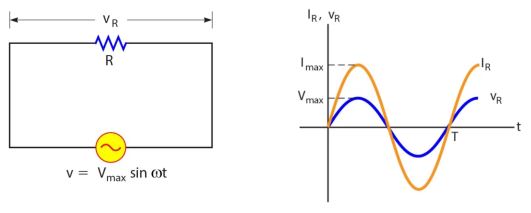
1. Rangkaian Resistor

Rangkaian resistor jika dihubungkan dengan arus bolak balik maka akan menghasilkan penurunan potensial listrik dalam rangkaian atau kata lain sebagai pembatas arus yang masuk.

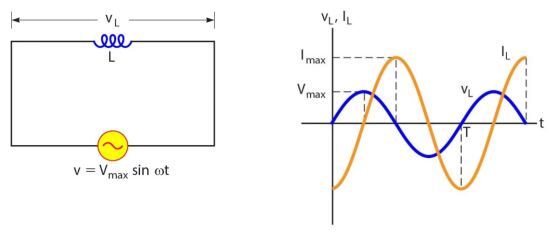
2. Rangkaian Induktor

Sebuah induktor juga memiliki nilai hambatan yang biasa disebut reaktansi  induktif saat dialiri arus bolak balik.

Nilai hambatan inductor ini bergantuk pada frekuensi sudut dari arus bolak  balik.

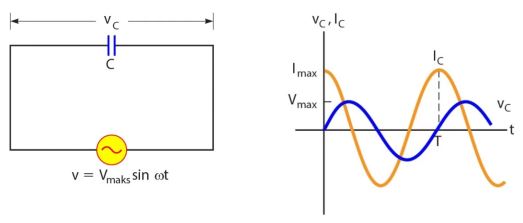
3. Rangkaian Kapasitor

Rangkaian kapasitor merupakan rangkaian yang unikdimana rangkaian ini  dapat menyimpan energi listrik sementara.

Kapasitor jika dialiri arus bolak  balik akan menimbulkan resistansi semu  atau biasa  disebut reaktansi kapasitif.

Nilai dari reaktansi kapasitif bergantung dari kapasitas kapasitor dan frekuensi  sudut.

Setelah kita mempelajari pengertian dan berbagai rangkaian arus bolak balik beserta diagramnya mari kita mulai menerapkannya pada persamaan matematis guna menyelesaikan persoalan yang terjadi pada kehidupan nyata.

Rumus Arus Bolak Balik

Terdapat beberapapersamaan matematis dalam arus bolak balik diantaranya yaitu:

Persamaan Umum

V = Vmax sin ωt

Rumus Arus Melalui Resistor

I_R = V_R/R

I_R = V_m/R sin ωt

I_R = I_m sin ωt

Rumus Tegangan Melalui Resistor

V_R = Vm sin ωt

Rumus Arus Melalui Induktor

I_L = V_m sin (ωt-1/2 π) /ωL

I_L = I_m sin (ωt-1/2 π)

Rumus Tegangan Melalui Induktor

V_L = Vm sin ωt

Rumus Arus Melalui Kapasitor

I_C = ω C V_m sin (ωt+1/2 π)

I_C = I_m sin (ωt+1/2 π)

Rumus Tegangan Melalui Kapasitor

V_C = Vm sin ωt

Dimana

• C = kapasitor
• L = Induktor
• R = Resistor
• I = Arus (A)
• V = Tegangan (V)
• ω = frekuensi sudut
• t = waktu (s)

RANGKAIAN SERI R-L-C

Rangkaian seri RLC terdiri dari empat kemungkinan komponen, yaitu rangkaian RC seri, RL seri, LC seri, dan RLC seri. Untuk lebih jelasnya, simak penjelasan berikut.

a. Rangkaian RC seri

Pada rangkaian RC seri, resistor dan kapasitor dirangkai secara seri dan dihubungkan dengan sumber tegangan bolak-balik seperti gambar berikut.

Dari gambar di atas terlihat bahwa komponen R dan C akan dilalui arus yang sama, yaitu I.

Secara matematis, persamaan yang terkait rangkaian RC seri ini dirumuskan sebagai berikut.

• Tegangan efektif

• Impedansi

• Besarnya sudut fase rangkaian

• Arus efektif

• Frekuensi resonansi RC

 

b. Rangkaian RL seri

Pada rangkaian RL seri, resistor dan induktor dirangkai secara seri dan dihubungkan dengan sumber tegangan bolak-balik seperti gambar berikut.

Dari gambar di atas terlihat bahwa komponen R dan L akan dilalui arus yang sama, yaitu I.

Secara matematis, persamaan yang terkait rangkaian RL seri ini dirumuskan sebagai berikut.

• Tegangan efektif

• Impedansi

 

• Besarnya sudut fase rangkaian

• Arus efektif

• Frekuensi resonansi RL

 

c. Rangkaian LC seri

Pada rangkaian LC seri, kapasitor dan induktor dirangkai secara seri dan dihubungkan dengan sumber tegangan bolak-balik seperti gambar berikut.

Dari gambar di atas terlihat bahwa komponen L dan C akan dilalui arus yang sama, yaitu I. 

Secara matematis, persamaan yang terkait rangkaian LC seri ini dirumuskan sebagai berikut.

• Tegangan efektif

• Impedansi

 

• Besarnya sudut fase rangkaian

• Arus efektif

• Frekuensi resonansi LC

d. Rangkaian RLC seri

Pada rangkaian ini, resistor, induktor, dan kapasitor dirangkai secara seri seperti gambar berikut.

Dari gambar di atas terlihat bahwa komponen R, L, dan C akan dilalui arus yang sama, yaitu I.

Oleh karena itu, pada komponen R akan muncul tegangan V_R, pada komponen L akan muncul tegangan V_L, dan pada komponen C akan muncul tegangan V_C. 

Diagram fasor impedansi untuk rangkaian RLC seri bisa Quipperian lihat pada gambar berikut.

Secara matematis, persamaan yang terkait rangkaian RLC seri ini dirumuskan sebagai berikut.

• Tegangan efektif

• Impedansi

 

• Besarnya sudut fase rangkaian

• Arus efektif

• Frekuensi resonansi RL

Dari pembahasan dan persamaan-persamaan di atas, dapat disimpulkan bahwa rangkaian RLC seri memiliki sifat berikut ini.

1. Jika X_L > X_C, rangkaian bersifat induktif di mana arus tertinggal oleh tegangan dengan beda sudut fase -90^o.
2. Jika X_L < X_C, rangkaian bersifat kapasitif di mana arus mendahului tegangan dengan beda sudut fase 90^o.
3. Jika X_L = X_C, rangkaian bersifat resistif di mana arus tertinggal oleh tekanan dengan beda sudut fase 0.  
   

 

Contoh Soal 1

Perhatikan gambar berikut.

Tentukan arus maksimum dan sifat rangkaian tersebut!

Diketahui:

Ditanya: Arus maksimum dan sifat rangkaian =…?

Pembahasan:

Untuk mencari arus maksimum dan sifat rangkaian, Quipperian harus mencari hambatan induktor, kapasitor, dan resistornya.

Hambatan induktor

Hambatan kapasitor

Impedansi

Arus maksimum

Oleh karena X_L < X_C, maka rangkaian pada soal tersebut bersifat kapasitif.

Jadi, arus maksimum yang mengalir dan sifat rangkaiannya berturut-turut adalah 12 A dan bersifat kapasitif.

Contoh Soal 2

Rangkaian RLC dihubungkan dengan tegangan arus bolak-balik. Jika induktansi pada rangkaian 10^-3 H dan frekuensi resonansinya 1.000 Hz, tentukan kapasitansinya dengan menganggap π² = 10!

Diketahui:

L = 10^-3 H

f = 1.000 Hz

Ditanya: C =…?

Pembahasan:

Untuk mencari kapasitansi, gunakan rumus resonansi.

Contoh Soal 3

Rangkaian RLC dengan R = 30 ohm, L = 40 mH, dan C = 50 µF dihubungkan dengan sumber listrik. Tentukan frekuensi resonansi pada rangkaian tersebut!

Diketahui:

R = 30 ohm

L = 40 mH

C = 50 µF

Ditanya: f =…?

Pembahasan: